With the help of Boyle's and Charles' laws, a relationship is established between the volume, temperature, and pressure of a fixed mass of a gas, which is called the gas equation.
Matter: Anything that has mass and occupies some space is called matter, matter exists in four states.
- Gas: the simplest form of matter.
- Liquid: Least abundant form of matter.
- Solid: The most abundant state of matter on earth.
- Plasma: Most abundant state of matter in-universe.
Note:- Only plasma is not the phase transition state of matter.
{tocify} $title={Table of Contents}
Properties of Gases
(I) Volume:- Gases do not have a specific volume and occupy all the available space.
(II) Shape:- Gases do not have a definite shape and take the shape of a container.
(III) Density:- Gases have a low density as compared is liquids and solids, gases bubble through liquid and tend to rise.
(IV) Diffusion and Effusion:- Gases can diffuse and effuse.
(V) Empty Spaces:- Gases can be compressed by applying pressure due to large empty spaces b/w molecules.
(VI) Expansion:- Gases expand on heating or by increasing available volume.
(VII) Joule Thomson Effect:- When the sudden expansion of a high or low-pressure gas occurs cooling takes place. It is the J.T. effect.
(VIII) Motion:- Molecules of a gas are in a state of constant motion. i.e. Transnational, Rotational, and vibration.
(IX) Forces:- Gases have very weak molecule forces or attractions.
(X) Kinetic Energy:- Gases have high kinetic energy and show effective collisions.
Pressures of Gases | Law of Gases
Force per unit area is called pressure. S.I unit of pressure Nm-2 or Pascal. Its unit is the atmosphere (atm.) The pressure of air that can support a 760 mmHg column at 0 ℃ gratitude of 45० sea level is called the atmosphere.
1atm = 760 mmHg = 76 cmHg = 101325 pascal = 101.325 KPa = 101325 Nm-2 = 14.7 Psi = 1013.25 millibar = 1.01325 bar.
Note:- Uses Pressure unit
1) Atmosphere (atm) is used for scientific work.
2) Pound inch -2 (Psi) is used for engineering work.
3) 1013.25 millibar is used by metrologies.
4) Nm-² and Pascal are S.I units of Pressure.
Colour and Odor of Gases
NO2 (Nitrogen Dioxide) is of reddish-brown colour, and hydrogen sulfide (H2S) has a rotten egg smell, H2, N2, and O2, He are colourless and odourless.
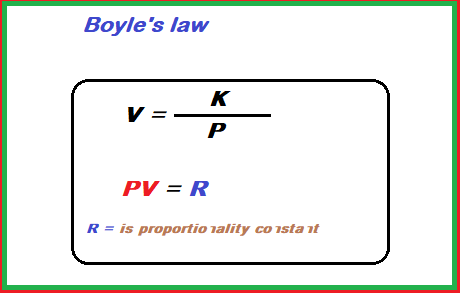
Boyle's Law
The volume of a given mass of gas, at constant temperature is inversely proportional to the pressure applied. V∝ 1 / P (T and n are constant)
The value of R is different for different amounts of some gases. Temperature increases continually K with increases. The product of pressure and volume of a gas at constant temperature is a constant quantity.
P1V1 = P2V2
Charles's law
The volume of a given mass of a gas is directly proportional to the absolute temperature when the pressure is constant. It is a quantitative relationship b/w the temperature and volume of a gas given by French scientist J. Charles in 1787.
V ∝ T
V = KT ( Pressure and no. of moles is constant)
K = V / T
The ratio of volume to temperature remains constant for the same amount of gas.
V1 / T1 = V2 / T2
Quantitative Definition:- At constant pressure the volume of a given mass of gas increases or decreases by 1 / 273 of its original volume at 0℃ for every 1℃ size or fall in temp.
Vt = V0 ( 1+ t / 273)
Where Vt = Volume at temp. T
t = Temp. on Celsius scale
V0 = Volume at 0 ℃
Avogadro's law
The equal volumes of all ideal gases at the same temp. and pressure contains equal numbers of moles.
V ∝ ղ
V = Rղ (Temperature and pressure are constant)
V1 / ղ1 = V2 / ղ2
Ek ∝ T
Tk. E ∝ NT
Absolute temp. is the measure of average translational kinetic energy. T ∝ K.E liquids translational + vibrant + rat + solids ⟶ Vibrational
Ideal gas law Definition and Formula
The gas obeys all gas laws under all values of temperature and pressure. Practically no gas exists.
Real Gas:- The gas that obeys all gas laws at a specific value of temperature and pressure.
General gas Equation
V ∝ 1/P
V ∝ T
V ∝ η
V ∝ ηT / P
V = RηT / P ( R is called the general gas constant)
Ideal Gas Constant (R)
The gas constant value of R depends upon. Units of pressure, Units of volume, and units of temperature.
R = PV / nT
Values and units of R can be calculated easily by using Avogadro's principle. units of Gas constant R= 0.0821 dm3atm /k mole (dm3 atm k-1 mol-1)
Significance:- The amount of energy that is required to change the temperature of one mole of gas by 1K. OR If we have one mole of an ideal gas at 273.16 k and one atm pressure and its temp. is increased by 1K, it will absurdly be 0.0821 dm3 atm of energy. dm3 atm is the unit of energy in this situation.
Note:- When pressure is given in Nm-2 and volume in m-3 the value of R used must be 8.3143 Jk-1mol-1.
Application of Ideal Gas Constant
There are two major applications of the ideal gas constant. 1- To determine the density of a gas. 2- To determine the molecule's mass of gas.
1. Density: density of H2O then decrease
PV = nRT ( n= mass / M. mass)
Mr
2. Molar Mass:- 22.414 dm3 = 6.02x1023 molecules, 1 dm3 = 2.68x1022 molecules.
P
Ideal and non-ideal behavior of gases
Ideal Gas:
* Ideal gas obeys all gas laws strictly under all conditions.
* The actual volume of an ideal gas is negligible as compared to the volume occupied by gas.
* No intermodular attraction or repulsion among gas molecules.
* It can not be liquefied.
Conditions for Ideal gas (Graph). High temperature and low pressure.
Non-Ideal Gas Behavior:
* If a graph is plotted between pressure on-axis and the comprehensibility factor Z = PV / KT on the Y-axis.
*For ideal gas straight line parallel to the pressure axis is obtained.
* For non-ideal gases, the graph is no longer parallel to the pressure axis.
Conditions for Non-ideality (Graph). High pressure and low temperature.
Non-ideality x I.M.F x Polar Gas
Kinetic Molecular Theory of Gases
To illustrate the behaviour of gases quantitatively, Bernoulli (1738) put a kinetic molecular theory of gases. This theory leads Clausius 1857 to derive kinetic equations and gas laws. The theory was later on elaborated and extended by Maxwell, who gave the law of distribution of velocities according to this.
" Molecules are in the form of groups having definite velocity range"
Boltzmann also contributed and studied disdain of energy among the gas molecules. van der Walls are also an important scientist in this field.
Postulates of Gas
1. Every gas consists of a large number of tiny particles called molecules.
2. Molecules move haphazardly, colliding with themselves and the walls of a container and changing their directions.
3. Pressure exerted on the walls of the container is due to collisions of molecules with walls collisions that are perfectly elastic.
4. Molecules have no forces of attraction.
5. The actual volume of gas is negligible as compared to the total volume of gas.
6. The effect of gravity is negligible due to repeated collisions of molecules.
7. The average K.E. of the gas molecules varies directly from the absolute temperature of a gas.
Kinetic Energy Equation or Kinetic Equation
Kinetic energy formula PV = 1/3mNc2
C2 is the average of Squares of possible velocities.
Root Mean Square Velocity: This equation is the quantitative relation between absolute temp. and gas molecules.
The PVT Relationship
With the help of Boyle's and Charles' laws, a relationship is established between the volume, temperature, and pressure of a fixed mass of a gas, which is called the gas equation. And also called the PVT Relationship.
Let the constant volume of gas be V, temperature T, and pressure P.
By Boyle's law
V ∝ 1/P (at constant temperature) ....(i)
By Charles' laws
V ∝ T ( at constant pressure) ......(ii)
By equations (i) and (ii)
V ∝ T/P
V = RT/P
PV = RT
Where R = 1 gm mole gas is the gas constant. If the number of gas molecules is n.
PV = nRT
This equation is called the gas equation of an ideal gas. From the gas equation, if a gas has volume V₁ at temperature T₁ and pressure P₁ and pressure P₂ and volume V₂ at temperature T₂.
P₁V₁/T₁ = P₂V₂/T₂
Gas Standard Conditions
The condition of temperature and pressure at which the volume of 1 gm mole gas is 22.4 litres is called the standard condition.
Temperature Pressure
0 °C 1 atm
273°C. 760 mm Hg
32°F. 29.93 Hg
491.69°R. 14.7 Psi
Partial Pressure
The pressure exerted by a gas in a mixture of gases is called the partial pressure of that gas.
Dalton Law of Partial Pressure
When two or more two gases that do not interact chemically are closed in a vessel at a certain temperature, the total pressure of the mixture of gases is equal to the sum of the partial pressures of those gases at the same temperature.
P = P1 + P2 + P3 + P4 ..........Pn
Partial pressure (P) = Mole fraction x Total pressure
Amagets Law of Partial Volume
Amaget's law of volume addition is in agreement with Dalton's law of pressure addition.
According to this, when two or more gases that do not react with each other are sealed in a vessel at the same temperature and pressure, the total volume of the mixture of gases is equal to the sum of the partial volumes of those gases at the same temperature and pressure.
V = V1 + V2 + V3 +.........
Suppose two or more gases that do not react chemically with each other at the same temperature and pressure are closed in a container. In that case, each gas occupies the same volume as it alone occupies in that container at the same temperature and pressure.
Also Read: What are Reactants in Chemistry
# Fundamentals of Chemistry notes | Chemistry basics for beginners
# Testing Methods Of Casein protein powder | Solubility of casein protein powder in water.
# Determination of Specific Gravity and Calculate
# Determination of saponification value | significance of ester value