Manometers are the oldest means of measuring pressure, it is the simplest, most accurate, and most accurate measuring instrument among all pressure measuring instruments. The manometer is used to measure pressure less than 30 psi. They are not reliable at high pressure. Commonly used manometers are as follows.
{tocify} $title={Table of Contents}
Types of Manometers
U-Tube Manometer
This is the simplest device of a Manometer, we use it for doing experimental work in the laboratory.
It is made of a small diameter U-shaped glass tube. The tube is fixed on a wooden board. Between the U-tube manometer, a scale is fixed on the same board. The U-tube is filled with a manometer fluid which is heavier than the process fluid. The common manometer fluid is filled with mercury.
U-tube Manometer Working Principle
A U-tube manometer is filled with a given fluid up to a certain height. The remaining of U-tube is filled with process fluid of density p the tubing. One limb of the manometer is connected to the upstream tap in a pipeline and another limb is connected to the downstream tap in the pipeline between which the pressure difference P1-P2 is needed to be measured.
Air if any is there in the line or tube connecting taps and the manometer is removed. At steady for a given flow rate on the scale reading of the manometer.
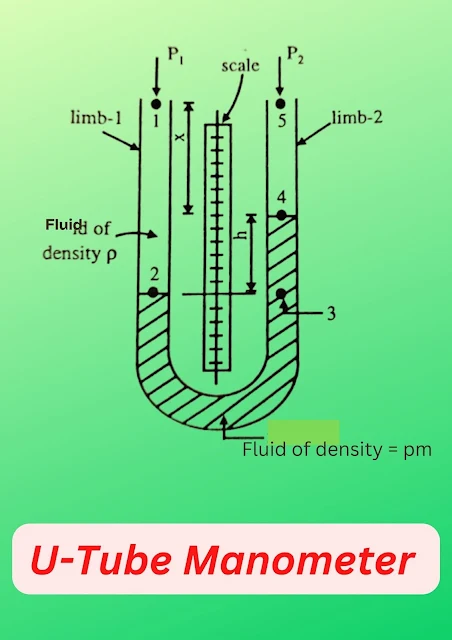
U Tube Manometer Derivation
Taken a U-tube manometer as shown in the upper diagram.
Let pressure P1 and P2 of the manometer.
To arrive at a relationship between the pressure (P1 and P2) difference (P1-P2) difference two limbs of the manometer in manometer fluid is (h), take pressures points 1,2,3,4, and 5.
Pressure point 1 = P1
Pressure point 2 = P1+(x +h)p.g
Pressure point 3 = pressure point 2
=P1+(x +h)p.g
Points 2 and 3 are at the same horizontal plane.
Pressure point 4 = P1+(x +h)p.g - h. pm.g
Where pm is the density of manometer fluid.
Pressure point 5 = P1+(x +h)p.g - h.pm.g - x.p.g
Pressure point 5 = P2
P2 = P1+(x +h)p.g - h.pm.g - x.p.g
P1 - P2 = ∆P = h (pm - p)g
Where ∆P is the pressure difference and h, is the difference in levels in the two arms of the U-tube manometer.
∆P = (P1 - P2) = h. pm.g
Limitation of U-tube manometer
When using a U-tube manometer, due to pressure, the liquid level rises in one arm and falls in the other arm, so no reference can be found.
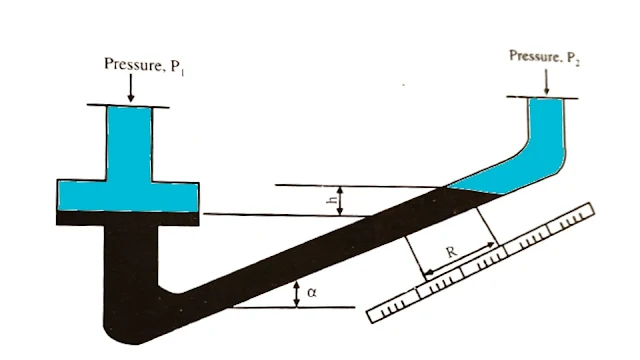
Inclined Manometer
When the pressure is very low, then an inclined manometer is used to measure it, in which one arm of the manometer is inclined in such a way that the vertical height (R) of the manometer moves some distance in the tube and Lets it is distance (h).
With the help of this, the low pressure can be easily read. The inclined Manometer has an angle of inclination of 5 to 10°.
h = R sin α
Where, α = angle of inclination
(P1 - P2) = R sin (pm - p). g
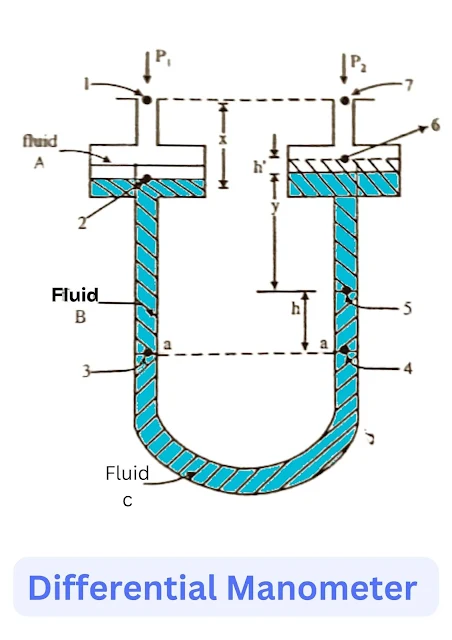
Differential Manometer/Two liquid Manometer/Multiplying Gauge
The differential manometer is used to measure low pressure. By this, we can measure the pressure difference between two objects inside a pipe. It consists of a simple U-tube type tube filled with liquid A and liquid C of density pa and pc, filled with a liquid B of density pm.
In large chambers are persecuted in the manometer so that the position of the meniscus points 2 to 6 does not change appreciably in the reading of R. The distance between points 1 and 3 may be considered equal to the distance between points 6 & 7 the total pressure difference can be calculated or following.
Differential manometer formula
Let the flowing fluids be A of density pA and manometer fluids be B and C of density pB and pC ( pC > pB) respectively (pA < pC).
The pressure difference between two points (1 and 7) can be obtained by writing down pressure at 1,2,3,4,5, and 7 given by.
P1 - P2 = h(pB + pA) g + h(pC - pB).g ----1.0
If the liquid level of liquid in two reservoirs is approximately the same then h=0 and equation 1.0 reduces to
P1 - P2 = h(pC - pB).g
The pressure at the level a-a in the picture must be the same in each of the limbs and therefore
P1 + [x.pA + hpA + y.pB + h.pB] g = P2+ [x.pA + h pB + h. pC] g
(P1 - P2) = h ( pB - pA) g + h( pC - pB) g.